Bayesian Multi-Logit Regression implemented in Tensorflow Probability
Bayesian Multi-Logit Regression is a probabilistic model for multiclass classification. This tutorial will make a prototype model in Tensorflow Probability and fit it with No-U-Turn Sampler.
Let’s start!
1. Model specification:
Multi-Logit regression for \(K\) classes has the following form:
$$p(y | x, \beta) = \text{Categorical}(y| \text{softmax}(x \beta))$$
With:
- \(x \): input features (row) vector \(x = [x_1,… x_D] \in R^D \)
- \(y \): the predicted outcome of the class label
- \(\beta \): weight matrix for \(K\) classes and \(D\) dimensions
The bayesian version of this model with pior:
$$ \beta \sim \mathtt{prior\_distribution(.)}$$
Approximate computing for the posterior predictive distribution:
- Monte Carlo draws beta samples from posterior: \(\beta^{(m)} \sim p(\beta | \mathtt{dataset})\)
- Compute the posterior predictive distribution: \(p(y |x, \mathtt{dataset}) \approx \frac{1}{M} \sum^M_{m=1} p(y | \beta^{(m)}) \)
2. Tensorflow Probability implementation:
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp
from sklearn.preprocessing import StandardScaler
# matplotlib
plt.style.use("bmh")
plt.rcParams["figure.figsize"] = 8, 8
# tensorflow probability
tfd = tfp.distributions
tfb = tfp.bijectors
tfpl = tfp.layers
dtype = tf.float64
# seed
np.random.seed(12)
tf.random.set_seed(12)
print(f"Tensorflow {tf.__version__}")
print(f"Tensorflow Probability {tfp.__version__}")
Tensorflow 2.8.0
Tensorflow Probability 0.16.0
2.1 Make synthetic data
def make_synthetic_data(train_ratio=0.6, val_ratio=0.2, n_samples_class=800):
"""Make synthetic data
"""
x = np.vstack([
np.random.multivariate_normal(mean=mean, cov=cov, size=n_samples_class)
for mean, cov in [([1, 1], 2 * np.eye(2)),
([4, 4], 2 * np.eye(2)),
([0, 4.5], 2 * np.eye(2))]
])
scaler = StandardScaler()
scaler.fit(x)
x = scaler.transform(x)
y = np.vstack([i * np.ones((n_samples_class, 1)) for i in range(3)])
idx = np.arange(0, x.shape[0], dtype=np.int32)
np.random.shuffle(idx)
pivot_1 = int(train_ratio * len(x))
pivot_2 = pivot_1 + int(val_ratio * len(x))
idx_train = idx[:pivot_1]
idx_val = idx[pivot_1:pivot_2]
idx_test = idx[pivot_2:]
x_train, y_train = x[idx_train, :], y[idx_train].reshape(-1)
x_val, y_val = x[idx_val], y[idx_val].reshape(-1)
x_test, y_test = x[idx_test], y[idx_test].reshape(-1)
return x_train, y_train, x_val, y_val, x_test, y_test
x_train, y_train, x_val, y_val, x_test, y_test = make_synthetic_data()
print(f"Train Dataset X {x_train.shape} with y {y_train.shape}")
print(f"Validation Dataset X {x_val.shape} with y {y_val.shape}")
print(f"Test Dataset X {x_test.shape} with y {y_test.shape}")
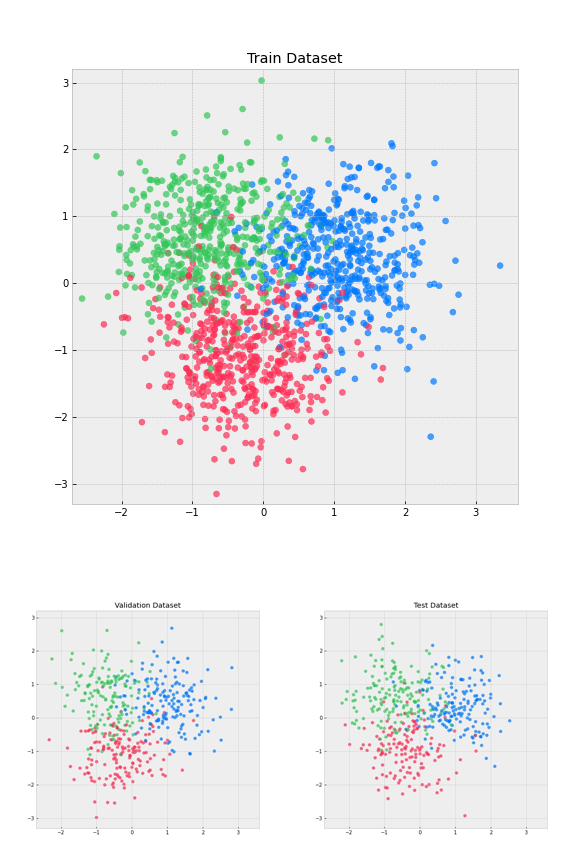
2.2 Visualize data
def color_func(y_i):
dict_color = {0: "#ff2d55", 1: "#007aff", 2: "#34c759"}
return dict_color[y_i]
def visualize_data(x, y, title=""):
plt.tight_layout()
colors = list(map(color_func, y.reshape(-1).tolist()))
plt.scatter(x[:, 0], x[:, 1], c=colors, alpha=0.7)
if title:
plt.title(title)
plt.xlim([-2.7, 3.6])
plt.ylim([-3.3, 3.2])
plt.savefig(f"{title}.png")
plt.show()
visualize_data(x_train, y_train, "Train Dataset")
visualize_data(x_val, y_val, "Validation Dataset")
visualize_data(x_test, y_test, "Test Dataset")
2.3 Bayesian Multi-Logit Model
def get_bayesian_multi_logit_model(beta_prior, x):
plate_notation = {
"beta": beta_prior,
"y": lambda beta: tfd.Categorical(probs=tf.math.softmax(x @ beta, axis=1),
dtype=dtype)
}
model = tfd.JointDistributionNamedAutoBatched(plate_notation)
return model
def bayesian_multi_logit_log_prob_fn(beta, y=y_train):
return bayesian_multi_logit_model.log_prob(beta=beta, y=y)
@tf.function(autograph=False, jit_compile=True)
def do_sampling(n_results, n_warm_up_step, target_log_prob_fn, init_state, step_size=0.1):
return tfp.mcmc.sample_chain(
num_results=n_results,
num_burnin_steps=n_warm_up_step,
current_state=init_state,
kernel=tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=target_log_prob_fn,
step_size=step_size
)
)
2.4 Sampling
beta_std_prior = 1
beta_prior = tfd.Normal(loc=tf.cast([[0] * 3] * 2, dtype),
scale=tf.cast(beta_std_prior, dtype))
bayesian_multi_logit_model = get_bayesian_multi_logit_model(beta_prior, x=x_train)
bayesian_multi_logit_model.resolve_graph()
(('beta', ()), ('y', ('beta',)))
n_results = 1000
n_warm_up_step = 500
random_sample = bayesian_multi_logit_model.sample()
beta0 = random_sample["beta"]
init_state = [beta0]
def bayesian_multi_logit_log_prob_fn(beta, y=y_train):
return bayesian_multi_logit_model.log_prob(beta=beta, y=y)
samples, nutkernel_result = do_sampling(n_results, n_warm_up_step,
bayesian_multi_logit_log_prob_fn, init_state)
2.5 Visualize with ArViz
posterior = {
# ArviZ expected: (chain, samples, **shape)
"β": samples[0].numpy().reshape(1,
n_results,
beta_prior.batch_shape[0],
beta_prior.batch_shape[1])
}
arviz_dict = az.from_dict(
posterior=posterior
)
az.plot_trace(arviz_dict)

az.plot_posterior(arviz_dict)
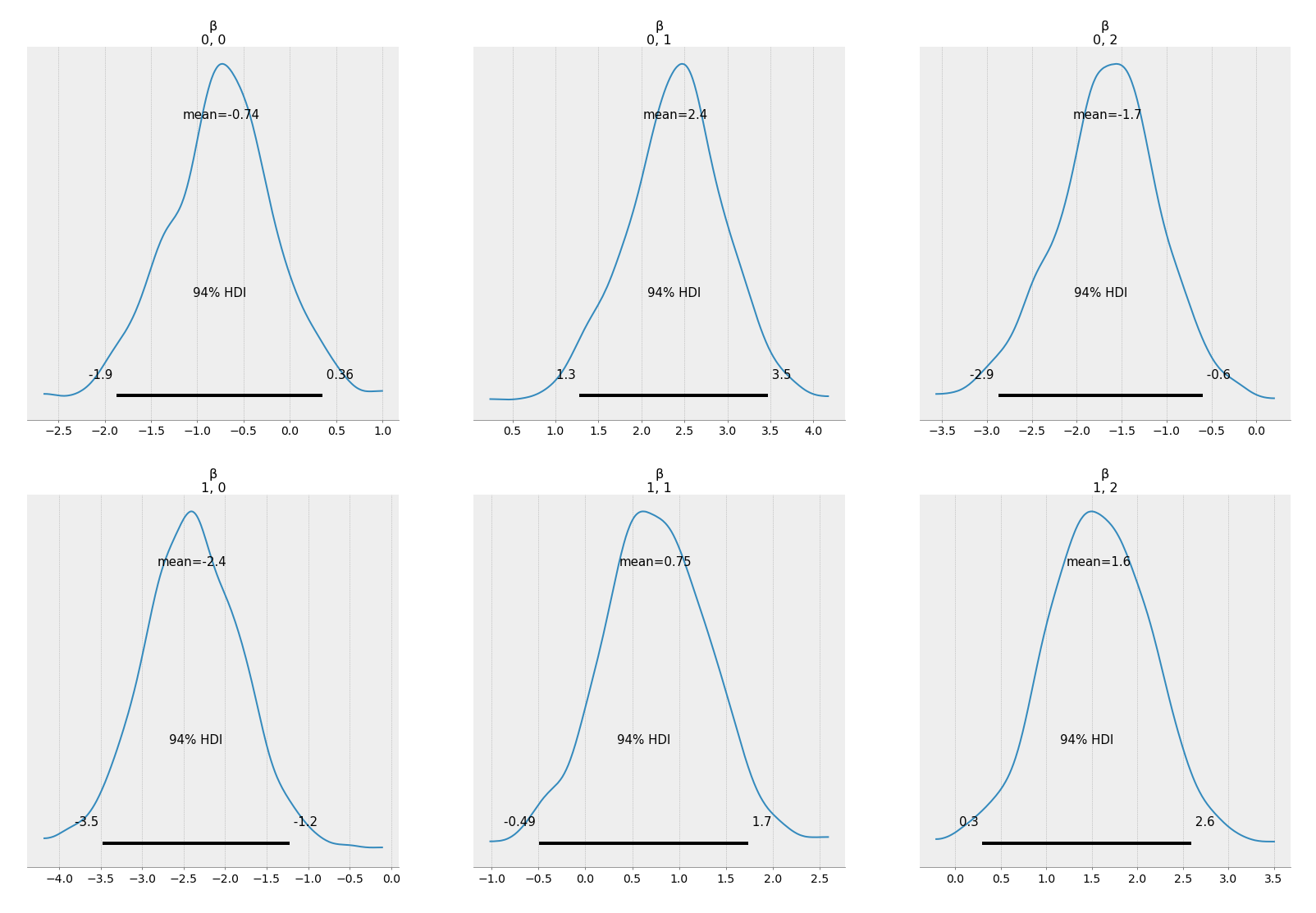
2.6 Posteirior predictive
def posteirior_predictive(model, x_vec, samples):
beta_samples = samples[0].numpy()
y_hat_prob = tf.math.softmax(x_vec @ beta_samples, axis=2)
y_hat_prob = y_hat_prob.numpy()
y_hat_approx_prob = np.mean(y_hat_prob, axis=0)
return y_hat_approx_prob
def classify(model, x_vec, samples):
y_hat_approx_prob = posteirior_predictive(model, x_vec, samples)
y_pred = []
for i in range(y_hat_approx_prob.shape[0]):
y_pred.append(np.argmax(y_hat_approx_prob[i]))
return y_pred
y_pred_train = classify(bayesian_multi_logit_model, x_train, samples)
y_pred_val = classify(bayesian_multi_logit_model, x_val, samples)
y_pred_test = classify(bayesian_multi_logit_model, x_test, samples)
print(f"Train Accuracy {(y_pred_train==y_train).mean()}")
print(f"Validation Accuracy {(y_pred_val==y_val).mean()}")
print(f"Test Accuracy {(y_pred_test==y_test).mean()}")
Train Accuracy 0.8666666666666667
Validation Accuracy 0.8604166666666667
Test Accuracy 0.8604166666666667
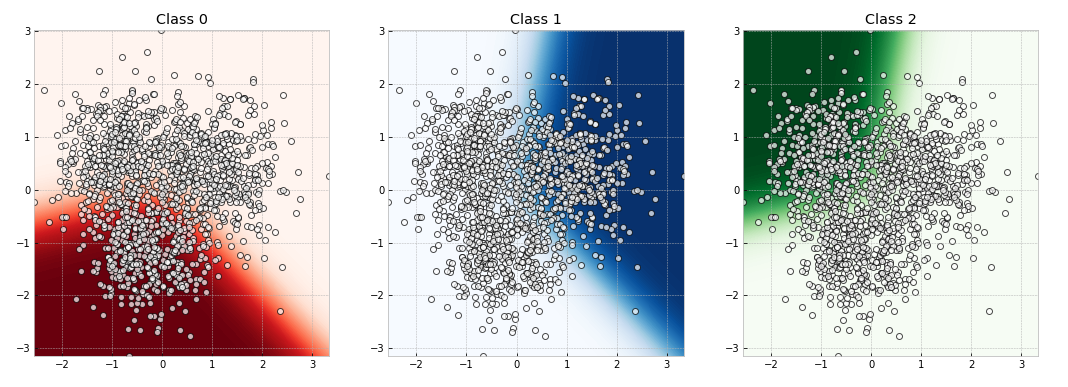
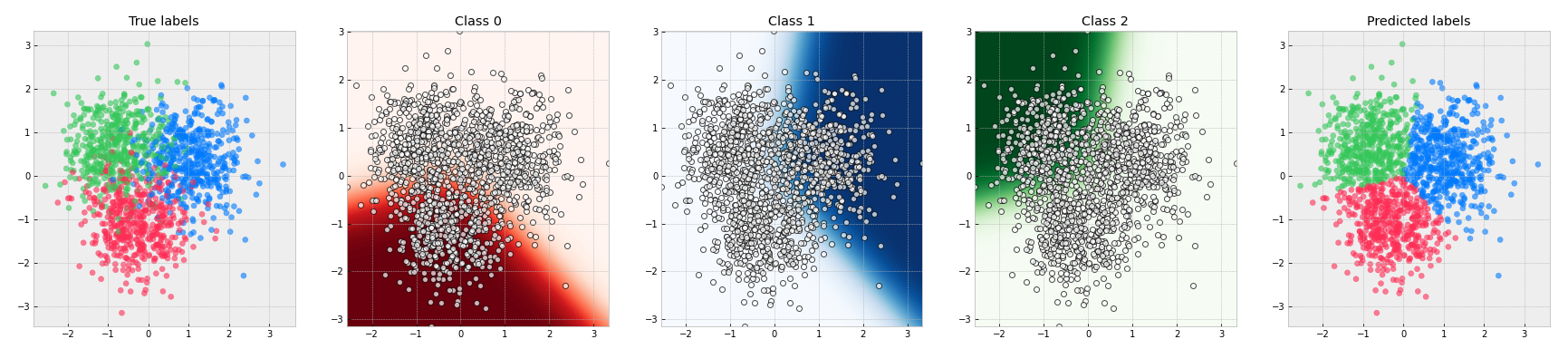
2.7 Visualize decision boundary
def visualize_decision_boundary(x=x_train, y=y_train):
n_point = 50
min_x = x.min(axis=0)
max_x = x.max(axis=0)
x0_lin = np.linspace(min_x[0], max_x[0], n_point)
x1_lin = np.linspace(min_x[1], max_x[1], n_point)
x0_grid, x1_grid = np.meshgrid(x0_lin, x1_lin)
x_contour = np.hstack([x0_grid.reshape(n_point ** 2, 1),
x1_grid.reshape(n_point ** 2, 1)])
z_contour = posteirior_predictive(bayesian_multi_logit_model,
x_contour,
samples)
z_0_grid = z_contour[:, 0].reshape(x0_grid.shape)
z_1_grid = z_contour[:, 1].reshape(x0_grid.shape)
z_2_grid = z_contour[:, 2].reshape(x0_grid.shape)
dict_grid = {0: z_0_grid, 1: z_1_grid, 2: z_2_grid}
fig, axes = plt.subplots(1, 3, figsize=(18, 6),
gridspec_kw={'width_ratios': [1, 1, 1]})
dict_cmap = {0: "Reds", 1: "Blues", 2: "Greens"}
for i in range(3):
axes[i].contourf(x0_grid, x1_grid, dict_grid[i],
cmap=dict_cmap[i], levels=100)
axes[i].scatter(x[:, 0], x[:, 1], c="white", linewidths=1,
edgecolors="black", alpha=0.7)
axes[i].set_xlim(min_x[0], max_x[0])
axes[i].set_ylim(min_x[1], max_x[1])
axes[i].set_title(f"Class {i}")
plt.show()
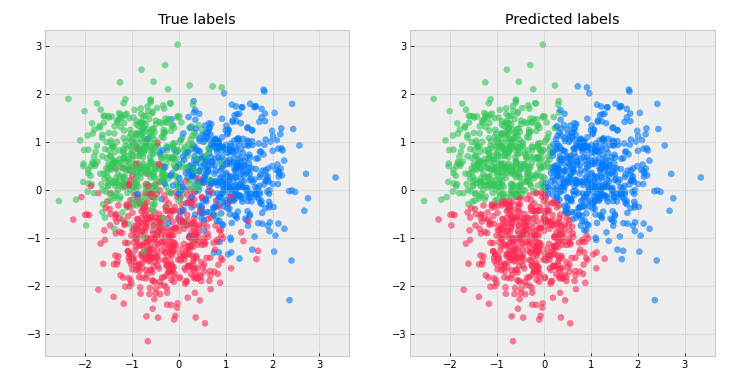
def visualize_classification(x=x_train, y=y_train):
fig, axes = plt.subplots(1, 2, figsize=(12, 6),
gridspec_kw={'width_ratios': [1, 1]})
axes[0].scatter(x[:, 0], x[:, 1],
c=[color_func(y_true_i) for y_true_i in y], alpha=0.6)
axes[0].set_title("True labels")
axes[1].scatter(x[:, 0], x[:, 1],
c=[color_func(y_pred_i) for y_pred_i in
classify(bayesian_multi_logit_model, x, samples)],
alpha=0.6)
axes[1].set_title("Predicted labels")
plt.show()
visualize_decision_boundary(x_train, y_train)
visualize_classification(x_train, y_train)